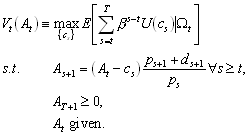John Hassler

June 16, 1997

EXAM
Macroeconomics I
5 points

I Short answers

Choose 5 out of the following 6. Preferably, you should not use more than 1 page per. Worth 10 points each.

  1. Evaluated the following statement "In a closed economy, a big national debt is no problem because the members of society owes the debt to themselves."
  2. In a standard Solow model, let Y=Ka N1-a with a =0.5. Let population growth rate be 0.04, the savings rate = 0.10 and depreciation 0.10. Compute the steady state consumption per capita.
  3. Consider an OLG model which has reached a dynamically inefficient steady state. Assume the government makes a transfers to the currently old and finance it by borrowing from the young. The government claims it never has to raise taxes but can roll over the debt forever. Could they?
  4. Is the following statement true, false or uncertain? "If an individual’s savings behavior is affected by risk one knows he cannot be risk-neutral."
  5. Evaluated the following statement. "The government should try to smooth labor taxes, i.e., keep them constant over time."
  6. Evaluated the following statement. "Evidence from the growth literature suggest that the share of income that goes to factors of production that can be accumulated is larger than the share that goes to physical capital, recorded in the national accounts."

II Problems

Choose 1 out of the following 2. Provide a strict formal argument. Worth 25 points

7. Asset Pricing

In this problem we are going to use the Lucas Asset Pricing model to price an asset (the tree in the original Lucas model). The economy consists of (infinitely) many individuals, indexed by the real numbers between 0 and 1. There is a competitive market for equally many trees, each producing a non-storable and stochastic output dt. In a particular period each tree produces the same amount, so there is no idiosyncratic uncertainty. By buying the tree in period t at price pt the holder gets next periods output dt+1 and can sell the tree at pt+1. The gross stochastic return is thus (pt+1+dt+1)/ pt. The representative agent’s consumption–investment problem in any period t can be represented by the value functions

1

where At is financial assets and ct is consumption.

1. Set up the Bellman equation for the consumption problem in . Make sure the notation is exact.

2. Derive the Euler equation.

We now assume, as in Lucas (1978) that humans and apple trees live for ever. Assume, furthermore, that U(c)=(1-a)-1 c1-a . Since there is no way to transfer real resources between periods it must be that ct=dt.

3. Use the assumptions above and Euler equation to derive an expression for the price of the Lucas asset.

Now assume that dividends, dt, follows

4. Given it is reasonable to guess that the asset price is linear in the current dividend. So that we can write pt=pdt with p, the price–dividend ratio, being constant for all t. Use this guess together with the Euler equation to get an explicit solution for p in terms of expectations of dt+1/dt.

5. Use the result that if e is N(0,s ) then

to express p as a function of problem parameters. What is the price–divident ratio when a equals unity and how does it change when a increases/decreases from unity?

(Hint; For any constant k, . Use this and to show that is a normal with mean zero and variance k2. What is the appropriate expression for k in this case?)

 

8. Education and Growth (Following Cutler, Poterba, Sheiner and Summers in Brookings Papers, 1990),

We are now going to analyze recent demographic changes in a closed economy Ramsey model where people work for a finite time and then retire. We will analyze the case where fertility unexpectedly falls permanently, which will decrease the support ratio, i.e., the share of workers in population. Let Pt and Nt be population and number of workers alive at time t. Define the support ratio At as Nt/Pt and the growth rates of At, P, and N by a, p, and n. Note that a=n-p.

Assume there is a CRS production function F(Kt,Nt) where K is non-depreciating capital. Let ct be consumption per capita (C/P) and kt be the capital to labor ratio (K/N). Let f(k)=F(k,1).

1. Show that the capital accumulation equation can be written

3

Let there be a social planner who maximizes the sum of discounted individual utility. He thus solves

4

2. State the Hamiltonian for the planning problem prior to the shock, i.e., for constant growth rates. Show that the necessary conditions for an optimum imply that

5

3. Draw the phase diagram for the planning problem in the c,k space prior to the shock with arrows that show the movement everywhere in the diagram and that include potential saddle paths.

4. Now analyze what happens after a sudden fall in n at time t0. Note that while n falls immediately to its new steady state it is going to take time for the support ratio to reach its new lower steady state. Draw one phase diagram for the initial phase, just after the fall in n, and one for the long run case. Assume that long run effects are dominated by the fall in A. Describe how consumption per capita and capital stocks per worker reacts dynamically to the shock. To simplify, assume that the dynamics are given by the phase diagram for the initial phase between t0 and some future date t1. From t1 and onwards, the dynamics are given by the long run phase diagram.

III Essay

Choose 1 out of the following 2. Emphasize discussion rather than formalism. Worth 25 points.

9. Convergence

Discuss what the modern theory of economic growth predicts about convergence of the income per capita of different countries or regions! Do the predictions of different theories square with the available empirical evidence?

10. Pension Systems

Discuss the effects of fully funded versus Pay-as-you-go pension systems in the OLG and the Ramsey model. Assume, at least in the primary discussion, that the economy is closed and has a perfect capital market.

A pass will require 60 points (out of 100) and a pass with distinction 80 points.

Good Luck!