Lecture notes for Macro I
Endogenous Growth
Prerequisites for Endogenous Growth
Take the simplest neo-classical growth model and assume away the exogenous growth rates. Can we anyway generate sustained long run growth? Let the CRS production function be
![]()
20
and capital accumulation
![]()
21
Now
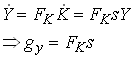
Now , what happens to gy as time goes to infinity. The RHS of is non-negative. As long as s is strictly positive, capital accumulation continues. So if s is kept positive FK falls forever since FKK <0. In other words, if F shows CRS in K and AL, then it shows DRS in K alone. If the Inada condition
![]()
then the economy thus is bound to approach zero growth due to and the fact that s is finite.
With depreciation or population growth we need that the limit in is large enough to account for depreciation and population growth.
What is the fix? We need to have a production function that shows CRS in factors of production that are produced (i.e., that are accumable). The most simple and straightforward way is to let the productivity index A depend on how much capital the economy has accumulated. We could think of this as a Learning by doing mechanism.
So in the simplest endogenous growth model we could assume that the level of knowledge, measured by A is given by
![]()
24
Substituting into the production function we have
![]()
25
From the CRS assumption we have
![]()
26
The term F(1,aL) is constant so output is linear in K alone, i.e., shows CRS in K alone. In some of the already classic articles by Romer and others the constant was called A. Then we can write Y=AK, thus these models go under the name AK-models.
The basic ingredient in endogenous growth models is thus to construct a social production function that has CRS in produced factors of production. There are basically to lines of models that achieve this,
Knowledge or Human Capital in the production function. Knowledge and/or human capital is surely producable as you hopefully experience during this course. If then the production function has CRS in capital and human capital together.
Increasing specialization. Since Adam Smith we know that increasing market sizes permits increasing specialization. So as production increases the economy may be more and more efficient. This may be another source of endogenous growth.
Growth rate in the simplest learning by doing (AK) model
Let the constant F(1,aL) be called A. Then we have
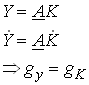
27
So the growth rate of the economy depends on the growth rate of capital which in turn depends on the net savings rate. With a given savings rate s
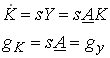
28
In this simple model it is easy to endogenize the savings decision. With CRRA preferences
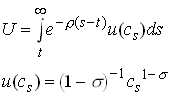
29
the Euler equation, which we can derive using Optimal Control, states that
![]()
30
where rt is the net return on savings. If this equals the full marginal return on capital (why should it not?) – rt = A so
![]()
The only saving rate which is consistent with and the transversality conditions is that the growth rate of consumption equals the growth rate of output. What would happen otherwise? So

32
Note that this model implies very simple dynamics – the economy is always in its steady state growth path. Shifts in some parameters or a shock to the capital stock implies an immediate jump to the new steady state growth path. Can you explain why?
Aggregate versus Private Knowledge
In the previous example there was no distinction between aggregate and private knowledge. This meant that the learning by doing effect of accumulating capital was fully internalized in the savings decision by the individuals. This may, reasonably, not be the case. Take the opposite view instead. Assume that there are an infinite number of identical small firms indexed by the rational numbers i on a unit interval [0,1]. Now that the production function for the individual firm is given by
![]()
33
The level of knowledge is proportional to the aggregate stock of capital and is identical to all firms.
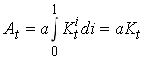
34
Now the aggregate production function can be written
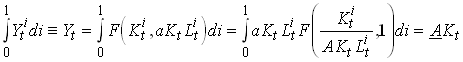
35
However, when a firm decides to increase its capital slightly, the effect that has on the aggregate capital stock and thus on the stock of knowledge is negligible. This since
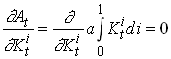
36
So the private return on capital is
![]()
37
which is smaller than the social which equals
![]()
38
Let, for example, the production function be
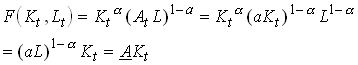
39
The private return to capital is in this case
![]()
40
Since this is the interest rate faced by consumers the Euler equation for consumers with CRRA utility gives
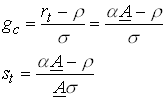
41
So we see that growth in this model is to low compared to the welfare maximum given by
R&D
In the previous examples knowledge was produced as a by-product of capital accumulation. We can easily change that and introduce a specific sector where knowledge is produced. So let
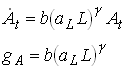
42
where aL is the share of labor that is allocated to knowledge accumulation. This sector could be thought of as an R&D sector or a schooling sector. The are some decreasing returns to scale in this sector if g is smaller than unity. The production function for output and the capital accumulation is given by
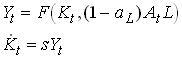
43
For now we assume that savings and the share of labor allocated to R&D is fixed and exogenous. Now lets define
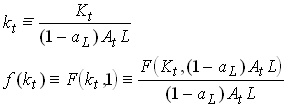
44
So, as in the Solow model
![]()
Now this reminds us about the Solow model and a steady state occurs when is zero. Let us look at a plot of the components in the RHS of .
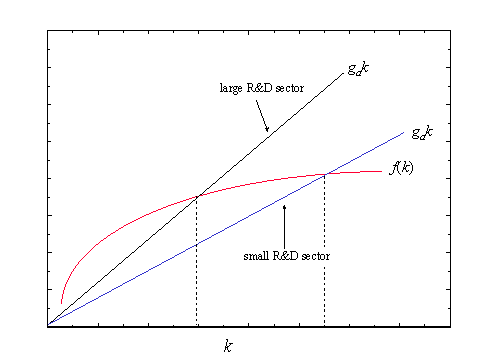
We see that a large R&D sector and thus a high growth rate of knowledge implies a lower steady state capital/effective labor ratio and vice versa. What would happen if we got a shift from a low to a higher share of labor in the R&D sector?
In this model the savings rate is unimportant for long run growth as in the Solow model. But, now growth is (almost) endogenous. To really explain growth we would like to let aL be determined within the model. This is the next step in the development of this model. We would like to have some firms who do the R&D and hire labor for this. Obviously we need to introduce some property rights for that purpose. Note that in such a model there is no reason to believe that growth is at its socially optimal level.
Growth from increasing specialization
Now let us turn to the other source of sustained growth – specialization. Let us think of an economy with two sectors. Final output which is produced using labor (with inelastic supply) and a range of intermediate goods. The latter are produced with capital only. The production function for the final good is
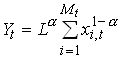
where each xi,t represents the amount of a particular intermediate input that is used at time t. Mt is the total number of intermediate inputs in use at t. We are going to look at symmetric equilibria where all xi,t are equal and denoted xt so
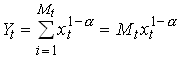
47
where we have normalized the labor supply to unity. The specification in implies that there is positive returns to specialization. Consider the case when we double the number of inputs but use each in half the amount. Output is then

48
Now look at the intermediate goods production sector. Here capital is transformed into intermediate goods by Mt firms. There is a fixed cost of running a firm (paid in capital) so the capital requirement of firm i which produces xi,t can be written
![]()
49
Now we assume that the final goods sector is competitive and that it buys intermediate goods so that its marginal product equals its price
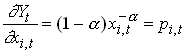
50
This is the inverse demand faced by the intermediate goods producing firms so their profits are
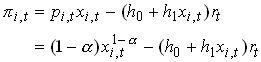
where rt is the user cost of capital (interest rate plus depreciation). From follows that the profit maximum for intermediate goods producing firms is
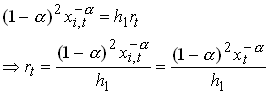
where the last equality comes from the assumption of a symmetric equilibrium. Now assume that there is no barriers to entry so profits in the intermediate goods sector are zero.
![]()
Lastly, we require that the capital market is in equilibrium so that supply of capital (which is given at any point in time) equals its demand. This implies
![]()
Substituting from into we get
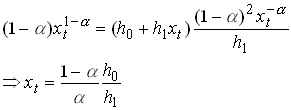
55
Lastly, substituting this into we get
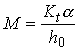
56
Substituting these results into the production function for aggregate output we get
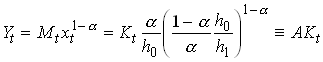
so we are back into the simple AK model. Now we just have to make some additional assumption about savings, for example that it is chosen optimally by individuals facing some interest rate, for example the one established at the capital market and given by if there are no capital income taxes. That savings rate determines the growth rate of capital which from is identical to the growth rate of output.