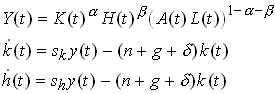
Some Evidence
The neo-classical growth model implies convergence. Growth should be inversely related to starting levels of GDP – poor countries should grow faster than rich. Weak or no correlation, however, is generally found between growth and initial GDP. But other parameters may differ between countries. A poor country could be poor because it is far below its steady state growth path (implying high growth) or because its steady state growth path is below other countries (implying same growth as richer countries). Differences in savings rates could explain differences in steady states.
Another failure of the standard Solow model is that the implied convergence rate appears to be too fast.
Now take an augmented Solow model with human capital.
88
You can then show that
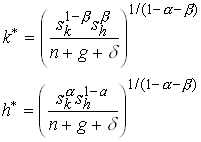
and
![]()
A log approximation of the speed of convergence close to the steady state gives
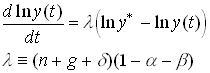
Note that the convergence rate decreases in b .
We can solve
![]()
92
or
![]()
This can be run as a regression. The growth rate should be negatively related to initial GDP. We must, however, control for differences in ln y*. Now substitute from and into . This yields
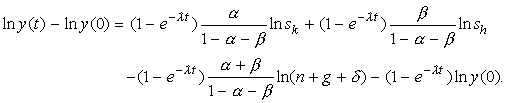
94
So we should include measures of the two savings rates plus n+g+d in the regression. Mankiw, Romer and Weil (1992) runs that regression on the Summers and Heston dataset (98 countries, 1960-85).
| Variable | coeff. | St.dev. |
| ln(GDP 1960) | -0.289 |
0.062 |
| ln(average investment rate) | 0.524 |
0.087 |
| ln(Secondary School enrollment 1960-85) | 0.233 |
0.060 |
| ln(n+g+d ) | -0.505 |
0.288 |
In a regression with the restriction that the coefficients on the two savings rates and n+g+d sum to zero a and b and l are identified. The estimated values are 0.48, 0.23 and 0.0142. This is substantially closer to what we believe is true in reality.
Conclusion.
Substantial evidence for conditional convergence.
The Solow model does a good job in explaning growth differences when differences in savings rates are taken into account.
The implied rate of convergence is reasonable when the production function includes human capital.
Barro (91) runs regressions of growth between 1960 and 1985 against initial GDP level and other variables that may affect growth or the level of the steady state growth path. The sample is 98 countries from Summers and Heston (1988).
| Variable | t-stat |
| GDP in 1960 | -6.3 |
| Secondary School enrollment 1960 | 3.8 |
| Primary School enrollment 1960 | 4.5 |
| Average Government spending ratio | -4.3 |
| Frequency of revolutions and coups | -3.1 |
| Rate of assassinations | -2.1 |
| Price distortions for investment goods | -2.7 |
We see that there is quite strong evidence in favor of conditional convergence. Also the other variables come in significantly with expected signs. Unclear if this is due to endogenous growth effects of different steady state growth paths with equal growth. The augmented Solow model cannot be rejected. (See Mankiw, Romer & Weil, 1992).