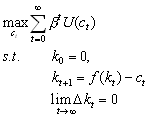
Problem set 5, MATFUII 1996

Consider the problem

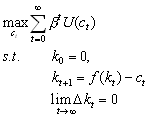
2. Set up the Bellman equation

3. Now assume that

and guess that the value function is given by

4. Solve for the consumption rule. Plug the solution into the Bellman equation. Show that this yields

5. Now construct a computer program (in Gauss for example) that iterates on the Bellman equation in order to find the value for A and B such that the Bellman equation is satisfied. Use

Hints;

Since there are only two free parameters in the value function we only need to evaluate it in two points, for example K=1 and 2. Now pick some initial guess for A and B, e.g., 1 and 2.

Then iterate on the following algoritm.

Plug those preliminary value into the RHS of the Bellman equation. Calculate the value of the RHS for K=1 and K=2, i.e., V(1) and V(2).

This yields new value for A and B from the equations B=V(1). A=(V(2)-B)/ln(2).

Plug these new values into the RHS and continue until you don’t get any changes in, say the 3^rd decimal place, of neither B nor A.

Using your computer program, find the values for A and B that makes the Bellman equation satisfied. Then check that your solution is OK by plugging in some other arbitrary values for k.

6. Do you think convergence should go faster or slower if we set the discountt factor to 0.99 instead? Test your answer with your computer program. What is the explanation for your results.