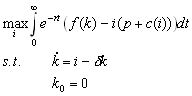
Problem for Friday December 6, 1996.
Consider the following investment problem.
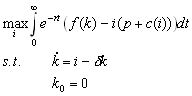
where f(k) is a production function, p is a (constant) price of investment goods, i is investments and c(i) is an installation cost. Now assume
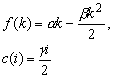
and that all parameters are strictly positive.
a) Write the current value Hamiltonian and the necessary conditions for an optimum.
b) Use the condition involving the derivative of the Hamiltonian with respect to the control variable to substitute for i. State your result in system of linear differential equations for the current shadow value qt and kt.
c) Draw a phase diagram of the system with k on the x-axis and q on the y-axis. Be careful when you draw the arrows. Indicate the solution for kt and qt for a finite value of T when the terminal condition is that kT is zero.
d) Assume T is infinite and the solution settles down to a steady state. Mark the solution to the problem.
e) Let the system be in a steady state. Assume that there is an unexpected fall marginal productivity, i.e., b increases, show what happens dynamically.
f) Which parameters determine the speed of convergence to the steady state.